Lineární funkce - výpočet a grafy

Grafem lineárních funkcí je přímka. Přímka je nekonečně dlouhá bezrozměrná rovinná křivka.

V aplikaci pro zobrazení lineární funkce si můžete vygenerovat graf podle svých potřeb. Graf lineární funkce si můžete po kliknutí pravým tlačítkem na obrázek uložit. Vysvětlení jednotlivých případů je vysvětleno v textu pod grafem lineární funkce.

Graf lineární funkce

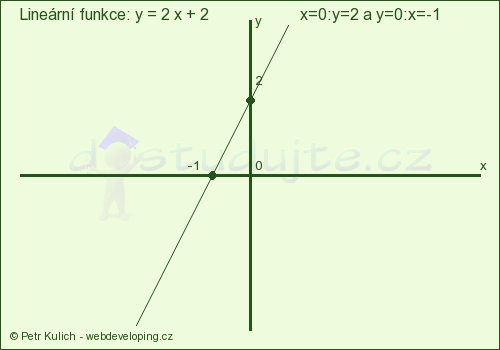
Aplikace slouží pro zobrazení lineárních funkcí
s celočíselným zadaním pro a a b od 0 do 99.

Připravujeme graf lineární funkce, kde budete možné zadávat desetinná čísla i zlomky.

Definiční obor a obor hodnot lineární funkce

Definiční obor lineárních funkcí zahrnuje všechna čísla, tj. D(f) = ( - ∞; + ∞).
Definiční obor všech funkcí čteme na ose x.

Obor hodnot lineárních funkcí zahrnuje také všechna čísla, tj. H(f) = ( - ∞; + ∞).
Obor hodnot všech funkcí čteme na ose y.

Obecný tvar rovnice přímky

f: y = a × x + b, kde a vyjadřuje sklon přímky a b vyjadřuje posun přímky po ose y
f: y = (+ a) × x + b, jestliže a je kladné, pak přímka prochází I. a III. kvadrantem
f: y = (- a) × x + b, jestliže a je záporné, pak přímka prochází II. a IV. kvadrantem
f: y = a × x + (+ b), jestliže b je kladné, pak je přímka posunuta do kladné části osy y, tj. nahoru
f: y = a × x + (- b), jestliže b je záporné, pak je přímka posunuta do záporné části osy y, tj. dolů

Příklady lineárních funkcí

Graf funkce je definován dvěma body, které se vypočítají z obecné rovnice přímky.

f₁: y = x
Do rovnice dosadíme x = 0, pak y = 0, dostáváme bod A [0;0]. Dále do rovnice dosadíme x = 1,
pak y = 1, dostáváme bod B [1;1]. Výsledná přímka prochází právě těmito dvěma body.

f₂: y = - x
Do rovnice dosadíme x = 0, pak y = 0, dostáváme bod A [0;0]. Dále do rovnice dosadíme x = 1,
pak y = - 1, dostáváme bod B [1; -1]. Výsledná přímka prochází právě těmito dvěma body.

f₃: y = 2*x
Do rovnice dosadíme x = 0, pak y = 0, dostáváme bod A [0;0]. Dále do rovnice dosadíme x = 1,
pak y = 2, dostáváme bod B [1;2]. Výsledná přímka prochází právě těmito dvěma body.

f₄: y = (1 / 4 ) * x
Do rovnice dosadíme x = 0, pak y = 0, dostáváme bod A [0;0]. Dále do rovnice dosadíme x = 4,
pak y = 1, dostáváme bod B [4;1]. Výsledná přímka prochází právě těmito dvěma body.

f₅: y = 6 * x + 2
Do rovnice dosadíme x = 0, pak y = 2, dostáváme bod A [0;2]. Dále do rovnice dosadíme x = 1,
pak y = 8, dostáváme bod B [1;8]. Výsledná přímka prochází právě těmito dvěma body.

f₆: y = 2 * x – 3
Do rovnice dosadíme x = 0, pak y = - 3, dostáváme bod A [0; -3].
Dále do rovnice dosadíme x = 1, pak y = - 1, dostáváme bod B [1; -1].
Výsledná přímka prochází právě těmito dvěma body.

Mám zájem o doučování